We have been using ultraviolet radiation as a means of disinfection for over a century. However, it has been the unfortunate events of the past year that have led to an explosion of interest in ultraviolet germicidal irradiation (UVGI) systems. From mercury vapour and pulsed xenon lamps to excimer lamps and ultraviolet LEDs, there have been, and continue to be, remarkable advances in ultraviolet radiation technology.

What we have yet to see, however, are comparable advances in our ability to model, and more importantly analyze the performance of, UVGI systems.

Architectural lighting designers have had the ability to model and analyze their designs for over fifty years. Using measured luminous intensity distributions provided by the luminaire manufacturers and architectural CAD models provided by their clients, they can quickly model the distribution of surface illuminance, taking into account both direct illuminance from the light sources and indirect illuminance due to interreflections from the environment surfaces.

Now, it is a straightforward process to adapt architectural lighting design software to UVGI applications. After all, both ultraviolet radiation and visible light are optical radiation that obey the same physical laws of optics. One of the advantages of doing this is that it becomes possible to predict the irradiances of surfaces that are hidden from direct view of the radiation sources. In Figure 1, for example, a mobile UV-C platform is being used to disinfect an operating theatre.

UVGI Design Software

It is also possible to model the UV-C dose, or fluence, of surfaces by considering multiple positions and dwell times for the mobile platform. Intelligent UV-C robots can be programmed to determine an optimal path for room disinfection. Using UVGI design software, it is possible to identify surfaces that may not receive a sufficient dose, and so flag them for enhanced terminal cleaning.

At the beginning of the COVID-19 pandemic when we were being advised to disinfect every surface, UVGI design software like this made perfect sense. However, we have known for over eighty years that aerosols are the primary transmission vector of respiratory diseases such as tuberculosis, measles, and influenza. Why it took nearly a year to acknowledge that this is also true for coronaviruses is a mystery, but the focus is now on the disinfection of air for interior spaces. This opens the door for the widespread adoption of UVGI systems using low-pressure mercury vapour lamps, ultraviolet-emitting LEDs, and far-UV excimer lamps.

We have, and are continuing to develop, the technology, but how can we model its performance? In particular, how can we model the spatial distribution of ultraviolet radiation in a volume of air?

Spherical Irradiance

We begin with a few definitions. Surface irradiance refers to the radiant power per unit area incident on a surface, regardless of the direction the radiation is coming from (Figure 2). For UVGI applications, it is measured in microwatts per square centimeter (mW/cm²).

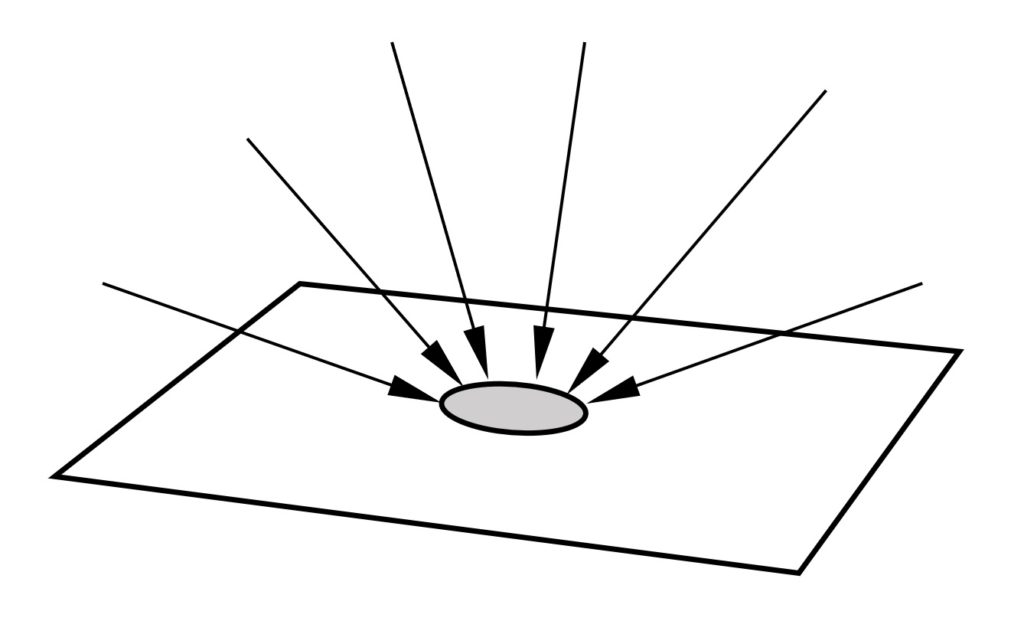
For aerosols and liquid droplets suspended in air, spherical irradiance refers to the radiant power per unit area incident on the aerosol droplet from all directions. For any given direction, the area of interest is the cross-sectional area of the spherical droplet. Integrating over all possible directions, we have the spherical irradiance, or fluence rate, of the droplet, also measured in microwatts per square centimeter (Figure 3).

It is important to note that these definitions consider radiation received both directly from radiation sources, and indirectly from surface reflections. While many common materials have low UV-C reflectances, some materials, for example sheet aluminum, can have reflectances as high as seventy percent.

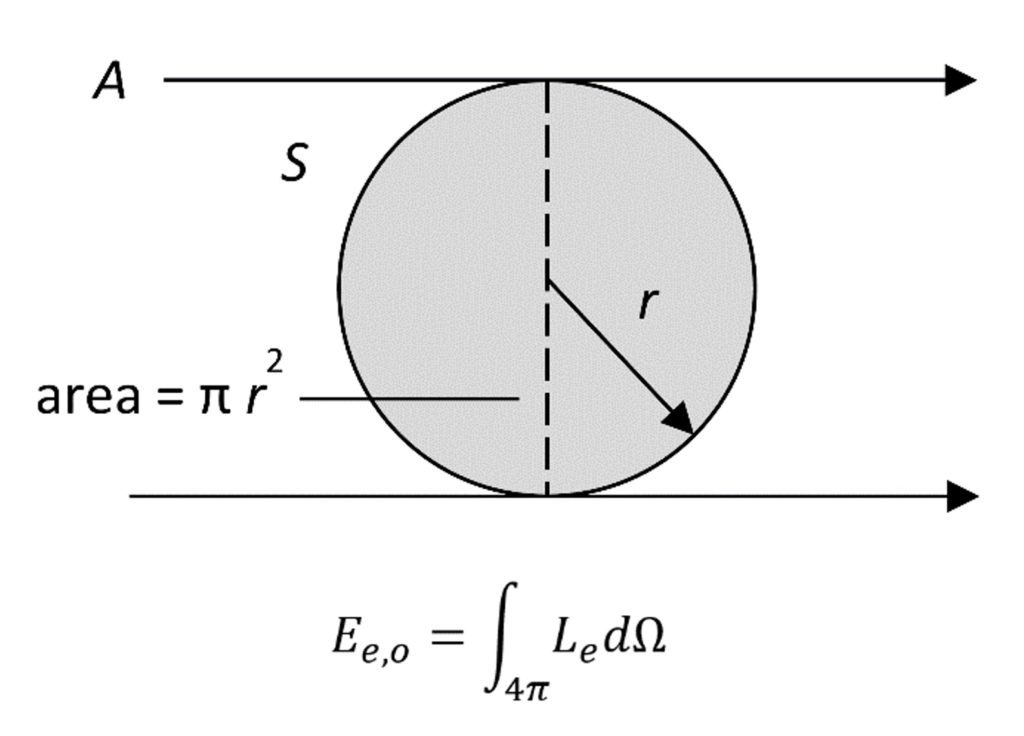
For UVGI applications, we are interested in the ultraviolet dose, or fluence, of the droplet, measured in millijoules per square centimeter. Unfortunately, there are no practical instruments to accurately measure ultraviolet fluence, apart from spherical actinometers – hollow quartz spheres filled with photoreactive chemicals such as ferrioxalate in solution.

We are however interested in not measuring, but modeling spherical irradiance in a volume of air, and so we need a virtual spherical irradiance (SI) meter.

Virtual SI Meters

From a mathematical perspective, it is easy enough to model the performance of spherical actinometers. However, the mathematics of spherical geometry are complex and difficult to solve in a reasonable amount of time. Moreover, we will need hundreds to thousands of spherical irradiance meters to model large volumes of air in complex architectural environments.

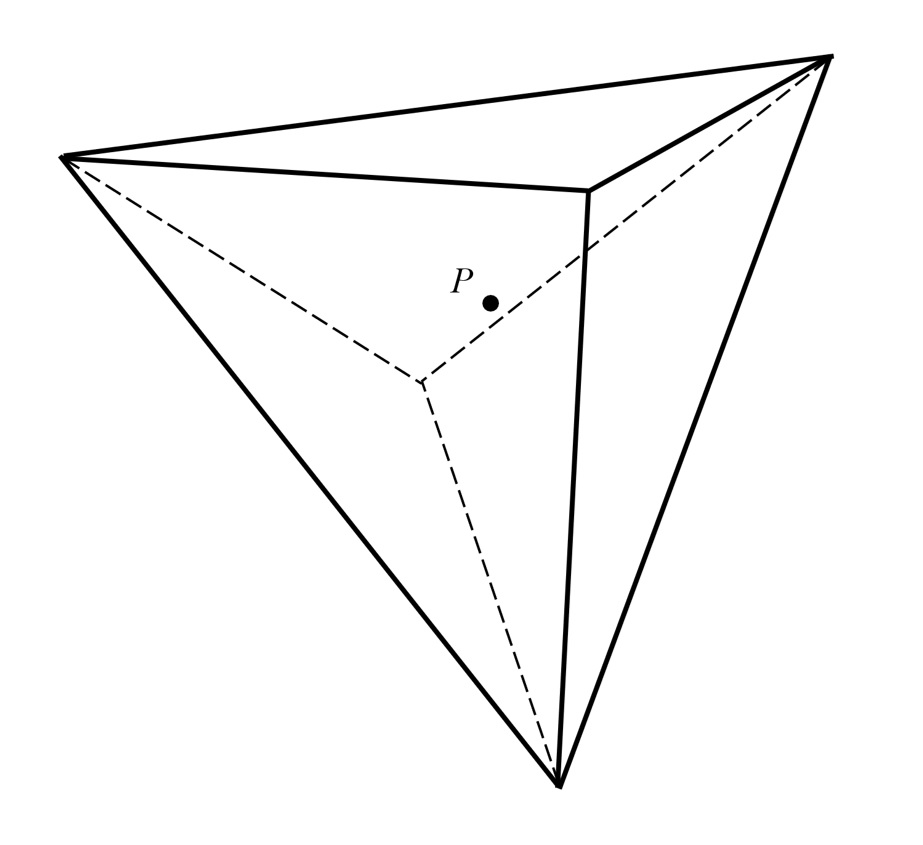
The solution is to replace the sphere with a six-sided dual cubic tetrahedron – imagine two three-sided pyramids mounted base-to-base (Figure 4). Like the sphere, each face will receive direct and indirect irradiance from its surrounding environment. Fortunately, the planar faces result in a much simpler mathematical model. This will allow us to position a three-dimensional array of meters in the virtual space in order to sample its ultraviolet radiation field.

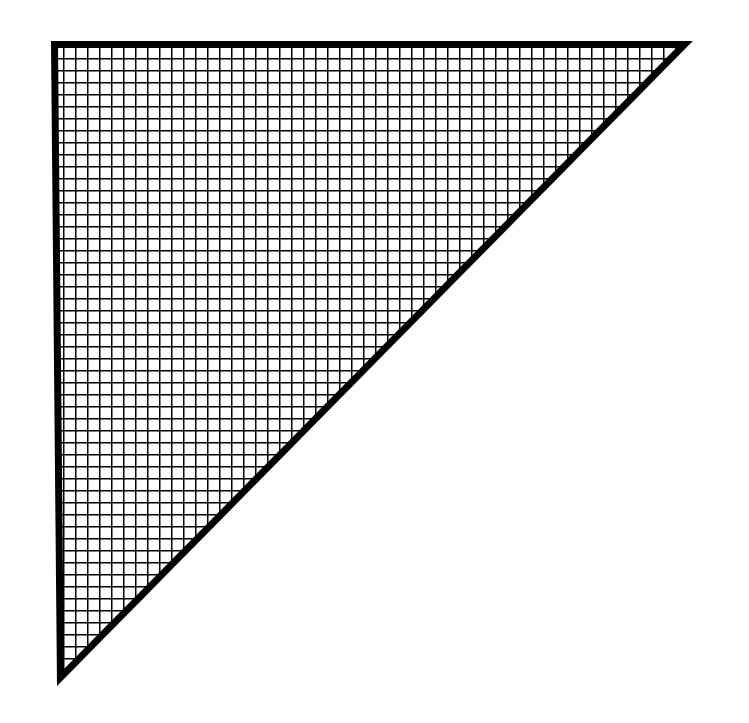
The calculation procedure is both simple and fast. Each dual cubic tetrahedron face is subdivided into a triangular array of elements, much like a computer display consists of a rectangular array of pixels (Figure 5). If we imagine being at the center of the meter, we have a 360-degree spherical view of the environment. In theory, we cannot tell whether we are viewing the actual environment or looking at six triangular computer displays surrounding us.

With this, we can project each visible object (or portion thereof for partially-hidden objects) onto the faces (Figure 6). This allows us to calculate the irradiance received from each visible object, and to sum the results to obtain the spherical irradiance.

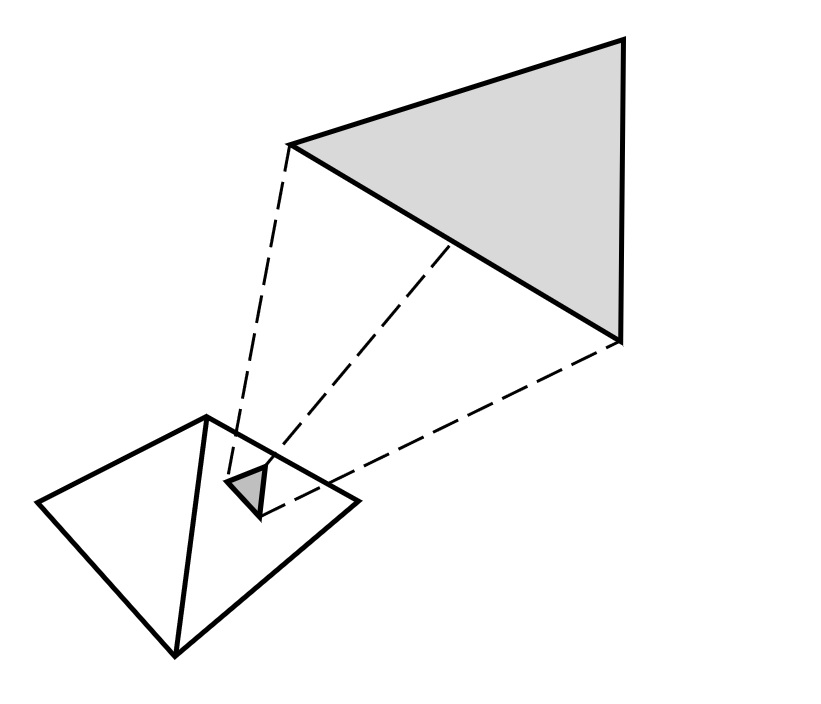
This is only a conceptual outline of the virtual spherical irradiance meter design. The design itself is based on radiative transfer theory, referred to in computer graphics research as “radiosity.” Developed in the 1980s for architectural visualization, it is fully applicable to UVGI modeling. (Today, the radiosity method forms the basis of Lighting Analysts’ AGi32 and ElumTools architectural lighting design software.)

The key point here is not the implementation of the meter design, but its speed.  Using a desktop computer, it takes only seconds to minutes to model thousands of spherical irradiance meters in complex environments.

Virtual spherical irradiance meters have a variety of applications, including the modeling of air disinfection systems. In Figure 7 for example, air flows through the serpentine channel of a recessed T-grid air sanitizer while being exposed to ultraviolet radiation emitted by seventy-two LEDs. From a design perspective, the average spherical irradiance within the channel is strongly dependent on the reflectance of channel walls. Modeling the system allows us to optimize the design.

FIG. 7 – Recessed T-grid air sanitizer design

Using CAD modeling, it is easy to represent even the most complex air-handling unit (AHU) geometries with their ultraviolet disinfection lamps (e.g., FIG. 8). Again, the spherical irradiance distribution within the units can be sampled with arbitrary density using a three-dimensional array of spherical irradiance meters.

The problem however is that the air flow within most air-handling units is turbulent. It is not the fluence rate that is important in deactivating pathogens, but the fluence. Turbulence affects how long the aerosols remain in the irradiance field, and so it must be accounted for in predicting the effectiveness of air disinfection.

Computational Fluid Dynamics (CFD)

To address this issue, it may therefore be necessary to employ computational fluid dynamic, or “CFD,” techniques to predict the time-averaged air flow through the air-handling unit (e.g., Figure 9). The predicted static irradiance field provides an input to any commercial or open-source CFD program.

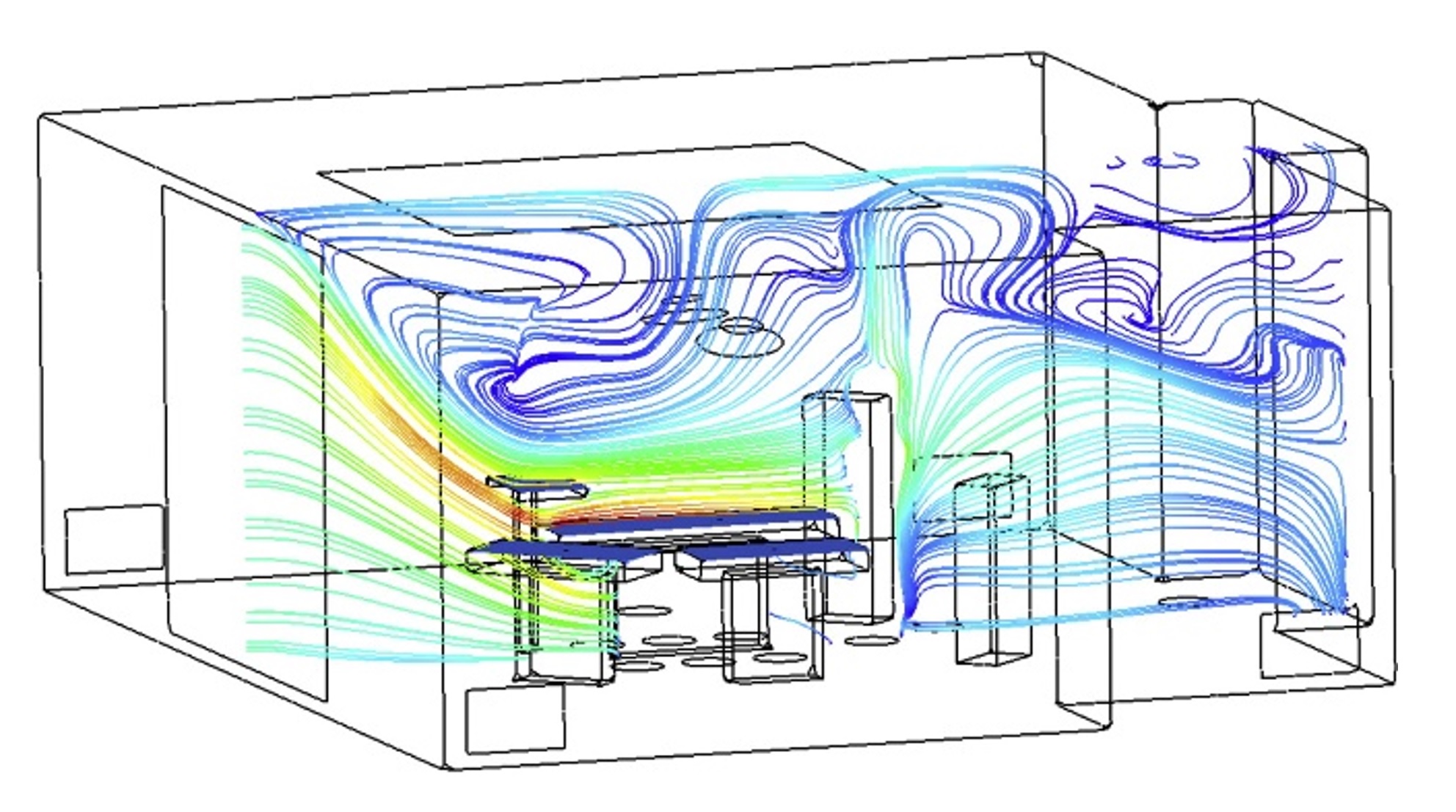
Unfortunately, mechanical engineers rarely employ CFD techniques when designing air handling systems for entire rooms, let alone complex architectural spaces such as hotel lobbies and theatres. Instead, building codes simply specify minimum air changes per hour.

This however will undoubtedly change in response to the current COVID-19 pandemic. Studies of infections in restaurants and other situations have highlighted the importance of differential air flow within enclosed spaces, and building codes will need to be revised to address this issue.

To summarize, it is possible to adapt existing architectural lighting design software to predict the ultraviolet irradiance of surfaces in complex environments, including both direct and indirect radiation. However, modeling air disinfection requires virtual spherical irradiance meters to be implemented within this software.

This article has outlined a novel approach that enables thousands of spherical irradiance meters to densely sample large volumes of air in these environments. The calculation times range from seconds to minutes, making the approach ideal for modeling air disinfection systems, air-handling units, upper-room applications with UV-C, and whole-room applications with far-UV.

Spherical irradiance meters are part of the solution in that they can predict fluence rates within air volumes. However, due to air flow turbulence in complex environments, computational fluid dynamic calculations will be needed to model the fluence that any aerosols may be exposed to.

Regardless, virtual spherical irradiance meters enable the modeling of UVGI systems. With them, we can design safe and effective air quality systems for the post-pandemic era.