Refinements to the Worthing Relationship – A Quantum Version of Wien’s Displacement Law
Eric Bretschneider, Ph.D.
Abstract
Wien’s Displacement Law is a simple equation that allows calculation of the peak wavelength for a black body light source as a function of temperature. However, not all uses of light are based on radiant flux. In particular, photobiology is based on the quantum or photon flux. In 1939 Worthing proposed a radiation law describing the emission of photons by black body sources. The Worthing Relationship has received little attention since then. The present study represents a modern computational evaluation of the Worthing Relationship.
Introduction
In physics, the term “black body” refers to an idealized body that perfectly absorbs all incident electromagnetic energy, regardless of wavelength. While perfect black bodies do not exist, the concept remains useful for many applications.
Prior to 1900, physicists were frustrated in attempts to derive an equation to predict the emission spectrum of a black body. There were two competing equations each of which was only able to predict a portion of a black body spectrum.
The first of these was Wien’s Radiation Law which was able to predict the spectrum of a black body at short wavelengths, but failed at longer wavelengths. The original formulation of Wien’s Radiation Law [Wien 1897] was given as:
where Bλ is the radiance, λ is the wavelength, T is the absolute temperature and C1 and C2 are empirically determined constants
Wien’s Radiation Law was accurate to within a tolerance of about 1% for λT < 3 x 106 nm·K. The values of C1 and C2 in this formulation were empirically determined. The modern formulation includes Planck’s constant and is given as:
where h is Planck’s constant, c is the speed of light, and kB is the Boltzmann constant
The second was the Rayleigh-Jeans Law which was able to predict the form of a black body spectrum at long wavelengths, but failed at shorter wavelengths. The Rayleigh-Jeans Law [Rayleigh 1900, Rayleigh 1905, Jeans 1905] was given as:
where R is the ideal gas constant
The Rayleigh-Jeans Law is accurate to within 1% for λT > 7.78 x 108 nm·K. A peculiar prediction of the Rayleigh-Jeans Law was that the total energy emitted per wavelength monotonically increased as wavelength decreased. This was termed “the ultraviolet catastrophe”.
In 1900, Max Planck derived the theoretical equation for the emission spectrum of a perfect black body.[Planck 1901] This has since become known as Planck’s Law and is given as:
where h is Planck’s constant, and kB is the Boltzmann constant
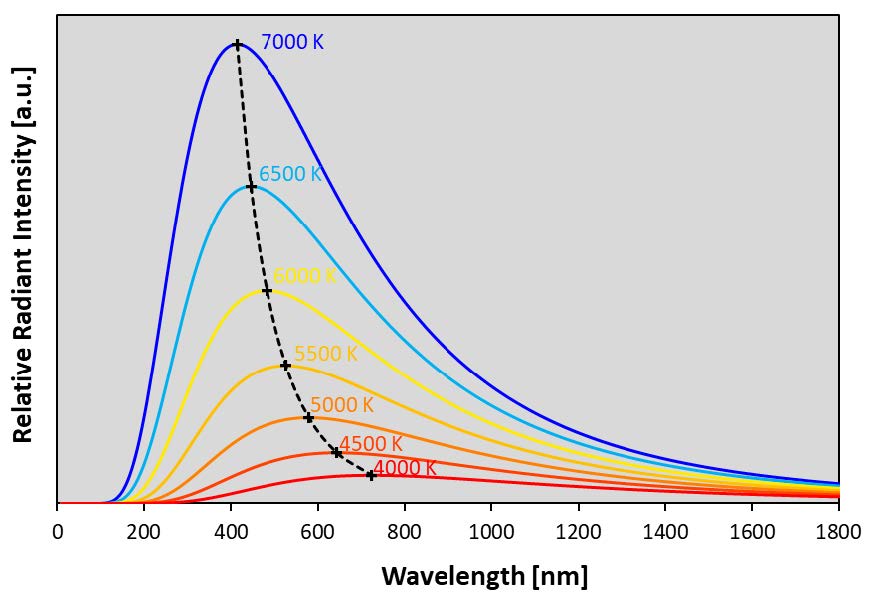
Using Planck’s Law, it is possible to predict the emission spectrum of a black body as a function of temperature. Figure 1 below shows the emission spectra for black body sources at various temperatures between 4000 K and 7000 K.
Figure 1. Planck’s Law spectra for black body sources between 4000 K and 7000 K.
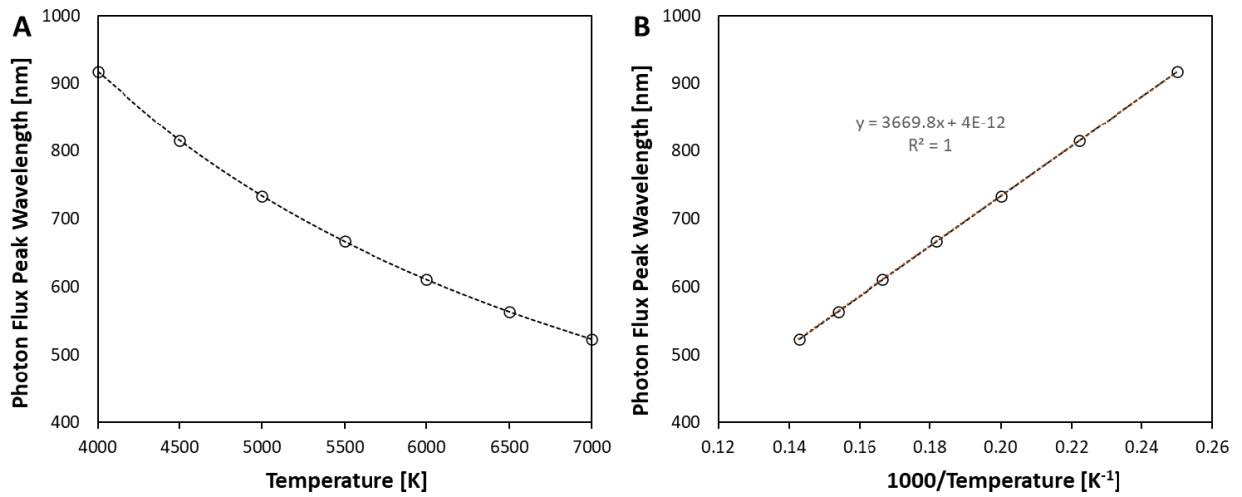
By inspection, it can be noted that Planck’s Law predicts that the peak wavelength decreases as temperature increases. This behavior is shown in Figure 2 below and is highly regular. The regularity is easily noted when the peak wavelength is plotted against the inverse of temperature.
Figure 2. Peak wavelength of a black body light source as a function of temperature (A) and inverse temperature (B).
This behavior was known prior to the derivation of Planck’s Law and was known as Wien’s Displacement Law. Wien’s Displacement Law stated that the peak wavelength of a black body light source was inversely proportional to the temperature and was given as:
where λmax is the wavelength for peak radiance [nm], and T is the absolute temperature [K]
While many applications using light deal with radiant flux (units of energy), applications related to biology are quantum in nature. That is to say they are based on absorption of photons of light. Since the energy of a photon is inversely proportional to its wavelength, the peak photon flux of a spectrum will always occur at a different wavelength than the peak wavelength calculated based on radiance.
In 1939 Worthing proposed a quantum version of Wien’s Displacement Law. [Worthing 1939] Using a derivation analogous to the theoretical formulation of Wien’s Displacement Law, Worthing derived the following equation for the peak photon flux wavelength:
where λmax,q is the wavelength for peak photon flux [nm]
Method
The spectral power distribution of an arbitrary black body light source can be calculated using Eq. 4 above. The resulting spectral power distribution can be converted to a spectral photon flux distribution by dividing the radiance at each wavelength by the photon energy for that wavelength. The energy of a photon is given as:
where λ is the wavelength in nm
In additional to the graphical results discussed below, calculations were carried out for black body temperatures between 1000 K and 12,500 K, at intervals of CCT-1 = 0.00001 K-1. This allowed equal weighting of results to determine the slope of the peak photon flux wavelength as a function of inverse temperature.
Spectra were analyzed over the range of 200 nm to 4200 nm at 1 nm intervals. The spectral power distribution and the spectral photon flux distribution were analyzed to determine the peak wavelength with a resolution of 1 nm.
Following this, the peak photon flux wavelength was plotted against reciprocal temperature and a linear fit was performed to determine the slope.
Results
In general, it is noted that the spectral photon flux distributions are similar in appearance to the spectral power distributions. However, it is important to note that the peak photon flux wavelength occurs at a higher wavelength than the peak wavelength. This is expected as the photon energy decreases with increasing wavelength, meaning that the number of photons at a constant energy increases as wavelength increases. For this reason, it is expected that for a smooth spectral power distribution, the peak photon flux wavelength.
The spectral photon flux distributions corresponding the spectral power distributions shown in Figure 1 above are shown in Figure 2 below.
Figure 3. Photon flux spectra for black body sources with temperatures between 4000 K and 7000 K.
The peak photon flux wavelength for these spectra as a function of temperature (and inverse temperature) is shown below in Figure 4. As expected, the relationship between peak photon flux wavelength and inverse temperature is linear.
Figure 4. Peak photon flux wavelength of a black body light source as a function of temperature (A) and inverse temperature (B).
The Worthing constant derived from this computational analysis differs slightly from the original value proposed by Worthing. The revised Worthing Relationship is given as:
where λmax,q is the wavelength for peak photon flux [nm], and T is the absolute temperature [K]
The value of the Worthing constant determined here is about 0.5% larger than the original value determined by Worthing.[Worthing 1939] Despite this difference, this new value represents a strong validation of Worthing’s original analytical derivation. In the intervening years since the publication of the Worthing Relationship, the values for fundamental constants have been revised over the years and are now known to a much higher precision than was the case in 1939. Using the currently accepted values for fundamental constants in Eq. 6 above yields a value of the Worthing constant of 3,669,694 nm/K which agrees with the calculated value to within 0.002% with the numerically calculated result.
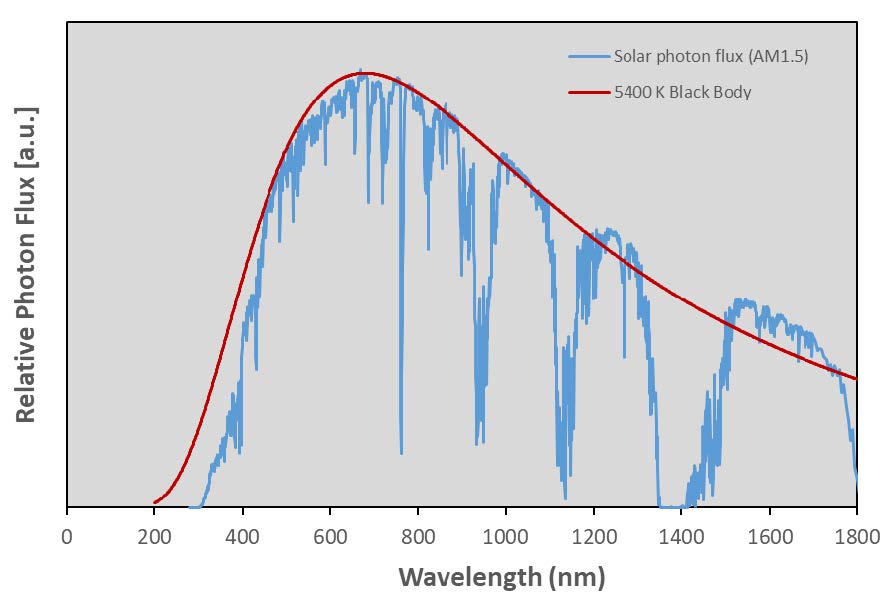
The Worthing Relationship can also be applied to solar spectra, or more generally to D-Series Illuminants. As an example, the AM1.5 solar spectrum [ASTM G173] is nominally a black body light source with a temperature of about 5400 K. Using the Worthing Relations, it is expected that a black body at 5400 K would have a peak photon flux wavelength of about 680 nm. In comparison, the actual peak photon flux in the AM1.5 spectrum occurs at 669 nm.
This difference is due to the nature of the solar spectrum which is not smooth and includes absorption and emission lines from elements in the solar chromosphere and atmospheric absorption. A comparison of the photon flux spectrum for a 5400 K black body and AM1.5 is shown below in Figure 5.
Figure 5. Relative solar photon flux (AM1.5) and photon flux for a 5400 K black body source. Wavelengths corresponding to peak photon flux are 669 nm and 680 nm respectively.
The revisions to the Worthing Relationship here are applicable to photobiological applications that utilize light sources that can be approximated as black body light sources. Recently, it has been proposed that hybrid light sources based on phosphor converted LEDs and traditional incandescent lamps be utilized for near infrared (NIR) phototherapy applications.[Reiter 2019]]
The Worthing Relationship allows designers to rapidly and easily calculate the peak photon flux wavelength for such applications. Importantly, it is noted that the equivalent black body temperature of incandescent light sources is generally in the range of about 2000 to 3000 K, which would correspond to peak photon flux wavelengths of about 1835 nm to 1223 nm. These wavelengths are outside of the operating range of commonly used spectroradiometers that utilize silicon-based detectors.
Conclusion
In summary, a revised value for the Worthing constant has been determined using currently acceptable values of fundamental constants. This analytically derived value was found to be essentially identical to the numerically determined value based on an analysis of spectral power distributions calculated using Planck’s Law.
Additionally, it has been shown that the Worthing Relationship is useful for estimating the peak photon flux wavelength for D-Series Illuminants and is also expected to be useful for designers of hybrid (phosphor converted LED supplemented by incandescent) light sources to determine the peak photon flux wavelength which may be outside of the wavelength sensing range of common spectroradiometers.
REFERENCES
Jeans 1905 – JH Jeans, “On the Laws of Radiation”, Proceedings of the Royal Society A. 76 (513): 545-552 doi: 10.1080/rspa.1905.0060
Planck 1901 – M Planck, “Ueber das Gesetz der Energieverteilung in Normalspectrum”, Annalen der Physik. 309:553-563 doi: 10.1002/andp.19013090310
Rayleigh 1900 – JWS Rayleigh, “Remarks Upon the Law of Complete Radiation”, Philosophical Magazine, 49, 301, 539-540 doi: 10.1080/14786440009463878
Rayleigh 1905 – JWS Rayleigh, “The Dynamical Theory of Gases and Radiation”, Natuer. 72, 54-55 doi: 10.1038/072054c0
Reiter 2019 – RJ Reiter, and S Zimmerman, “Melatonin and the Optics of the Human Body”,
Melatonin Research, 2, 138-160 doi: 10.32794/mr11250016
Wien 1897 – HW Wien, “On the Division of Energy in the Emission-Spectrum of a Black
Body”, Philosophical Magazine. Series 5. 43 (262): 214-220 doi: 10.1080/14786449708620983
Worthing 1939 – AG Worthing, “Radiation Laws Describing the Emission of Photons by Black
Bodies”, JOSA, 29, 97-100 doi: 10.1364/JOSA.29.000097

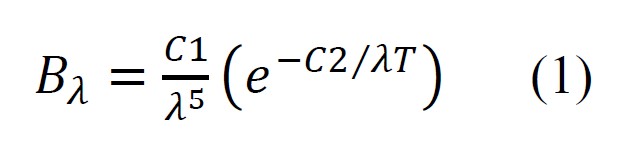
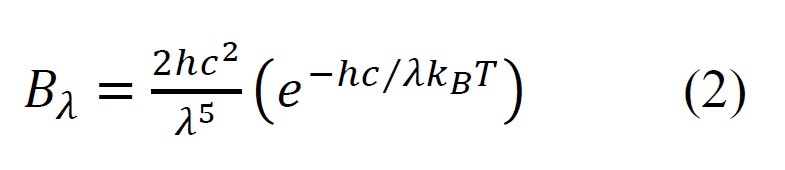
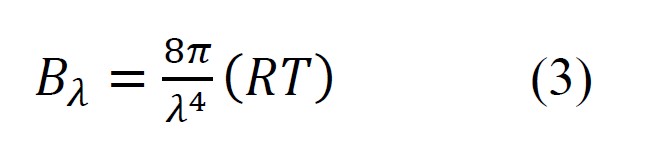
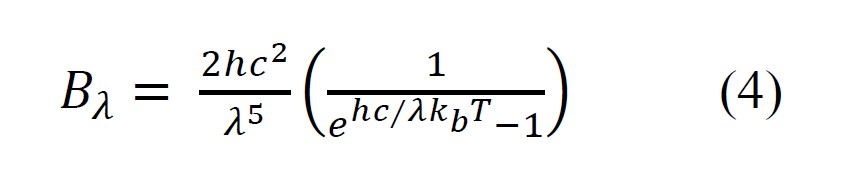
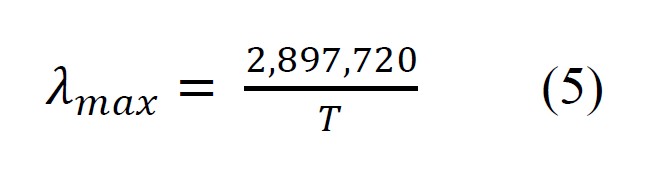
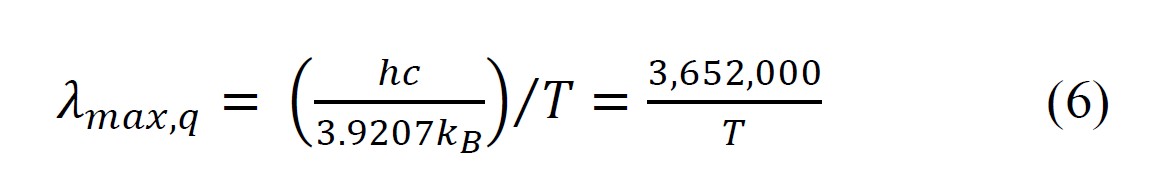
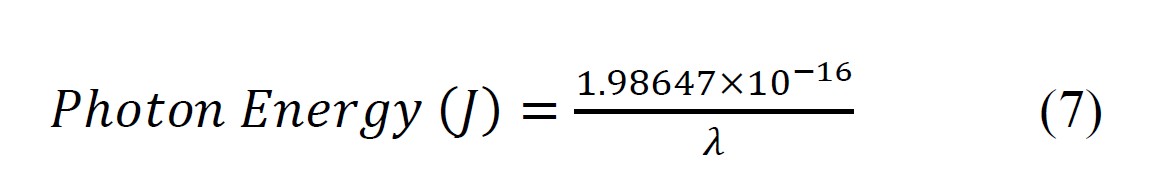
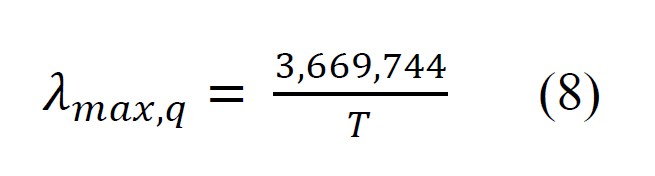
0 Comments