We have been using ultraviolet radiation as a means of disinfection for over a century. However, it has been the unfortunate events of the past year that have led to an explosion of interest in ultraviolet germicidal irradiation (UVGI) systems. From mercury vapour and...
Ultraviolet Radiation
Image by Freepik
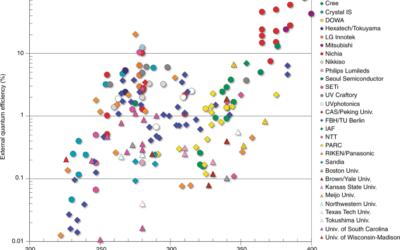
Defining Far-Ultraviolet
In these uncertain times, there is increasingly persuasive evidence that “far-UV” radiation is effective in inactivating the SARS-CoV-2 virus and other pathogens, but without the health risks of germicidal ultraviolet radiation. Unfortunately, this technology has some...
Ultraviolet Radiation & Viral Misinformation
Let me begin with a smorgasbord of headlines: 99.9% of Covid-19 virus dead in 30 seconds with UV LEDs, says Tel Aviv research (www.malaysianow.com) UV-emitting LED lights found to kill coronavirus (www.sciencedaily.com) Study reveals UV LED lights effectively kill a...
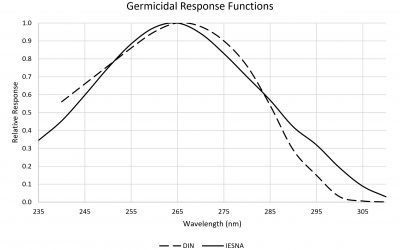
Ultraviolet Radiation Terminology
A word of caution: I am going to be annoyingly pedantic here, but with good reason. The lighting industry has a century-long history of introducing unfamiliar technologies using familiar terminology. We later come to regret our choice of words when it becomes...
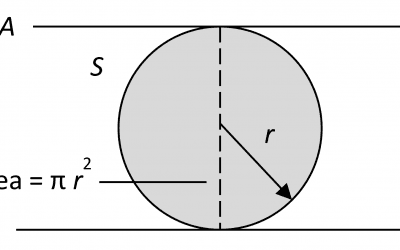
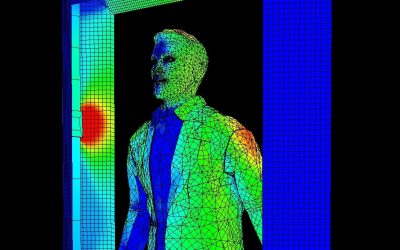
Spherical Irradiance and Aerosols
Lighting designers will be familiar with the illuminance of a planar surface, which is measured in lumens per square meter (or foot). The irradiance of a planar surface by a germicidal radiation source is conceptually the same, except that it is measured in watts per...
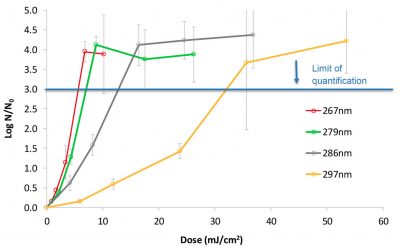
Designing an Ultraviolet-C Disinfection System
Recent germicidal light sources include UV-C light-emitting diodes and pulsed xenon discharge lamps, but there is a newcomer on the block that has gained considerable media attention: far-ultraviolet excimer lamps. What does it take to design a UV-C disinfection system using far-UV radiation?
Ultraviolet Disinfection for Consumers
In these unfortunate times, it seems that everyone is looking for ways to help with the COVID-19 crisis. From a lighting designer’s perspective, one solution is obvious: ultraviolet radiation. We have known about the disinfectant properties of ultraviolet radiation...
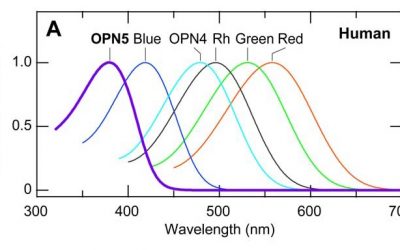
Seeing Ultraviolet
Ian Ashdown, P. Eng., FIES, Senior Scientist, SunTracker Technologies Ltd. Published: 2015/10/26 UPDATE 15/11/08 - The following text briefly notes that some people can see near-ultraviolet radiation following cataract surgery due to the UV transmittance of...